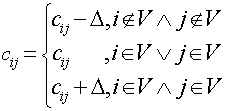Hungarian Algorithm

아래 글 참조

Assignment Problem and Hungarian Algorithm

Problem Statement

가장 대표적으로 $N$명의 사람에게 $N$개의 일을 담당하는 문제를 생각해보자. 각 사람은 1개의 일을 담당할 수 있으며 이에 대한 $cost$가 발생한다. 그러면 기업 입장에서 목표는 이 비용을 최소화하며 $N$개의 일을 배치해야 한다.

아래는 위 설명을 식으로 설명한 것이다.

$\{c_{ij}\}_{N\times N}$: cost matrix, where $c_{ij}$: cost of $i$ to perform job $j$.

$\{x_{ij}\}_{N\times N}$: resulting binary matrix, where $x_{ij} = 1$ if and only if $i_{th}$ worker is assigned to $j{th}$ job.

$\sum_{i=1}^{N}{x_{ij}} = 1$, $\forall i\in \overline{1, N}$: one worker to one job assignment.

$\sum_{i=1}^{N}{x_{ij}} = 1$, $\forall j\in \overline{1, N}$: one job to one worker assignment.

$\sum_{i=1}^N{\sum_{j=1}^N{c_{ij}x_{ij}}} \rightarrow min$: total cost function.

우리는 이 문제를 그래프 문제로 바꿔 생각할 수 있다. $N$명의 사람에게 $N$개의 일에 대한 $cost$가 주어졌다고 생각하면 각 $N$명의 사람에게 $N$개의 일이 간선으로 연결되어 있어 총 $N*N$개의 간선이 연결된 그래프로 표현할 수 있다. 아래 예시를 보자.

General Description Of The Algorithm

이러한 문제를 할당문제라고 한다.

이 문제를 foolish하게 해결하면 $O(n!)$이면 해결 할 수 있다. bfs, dfs로 순열을 찾고 이에 대한 cost를 계산해 최소값을 찾는다.

쉽게 할 수 있지만 문제를 해결하기에 적합한 시간복잡도는 아니다.

효율적인 방법의 알고리즘을 보여줄 텐데 하나는 쉽고 빠르게 $O(n^4)$이고 다른 하나는 구현이 복잡하지만 $O(n^3)$이다.

$O(n^4)$ Algorithm Explanation

이분 그래프로 이 문제를 다루겠다.

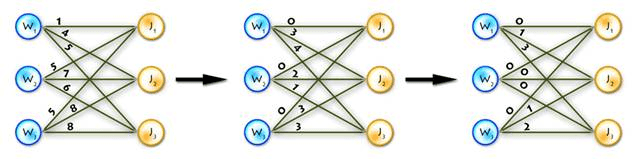
Step 0)

1. For each vertex from left part(workers) find the minimal outgoing edge and subtract its weight from all weights connected with this vertex. This will introduce 0-weight edges (at least one).
2. Apply the same procedure for the vertices in the right part (jobs).

실제 이 순서는 필요하지 않지만 main cycle 수를 줄일 수 있다.

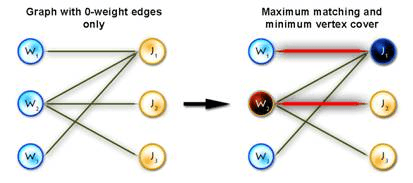
Step 1)

1. Find the maximum matching using only 0-weight edges (for this purpose you can use max-flow algorithm, augmenting path algorithm, etc.).
2. If it is perfect, then the problem is solved. Otherwise find the minimum vertex cover $V$(for the subgraph with 0-weight edges only), the best way to do this is to use Köning’s graph theorem.

Step 2)

Let $\triangle min_{i \notin V, j \notin V}{c_{ij}}$ and adjust the weights using the following rule:

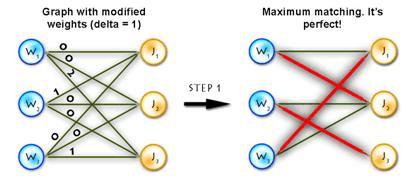
Step 3)

Repeat Step 1 until solved.

But there is a nuance here; finding the maximum matching in step 1 on each iteration will cause the algorithm to become $O(n^5)$. In order to avoid this, on each step we can just modify the matching from the previous step, which only takes $O(n^2)$ operations.

It’s easy to see that no more than $n^2$ iterations will occur, because every time at least one edge becomes 0-weight. Therefore, the overall complexity is $O(n^4)$

$O(n^3)$ Algorithm Explanation